Impact of geostatistical nonstationarity on convolutional neural network predictions

Convolutional neural networks (CNNs) are gaining tremendous attention in subsurface studies due to their ability to learn from spatial image data. However, most deep learning studies in spatial context do not consider the impact of geostatistical nonstationarity, which is commonly encountered within the subsurface phenomenon. We demonstrate the impact of geostatistical nonstationarity on CNN prediction performance. We propose a CNN model to predict the variogram range of sequential Gaussian simulation (SGS) realizations. Model performance is evaluated for stationarity and three common forms of geostatistical nonstationarity: (1) large relative variogram range-related nonstationarity, (2) additive trend and residual model-related nonstationarity, and (3) mixture population model-related nonstationarity. Our CNN model prediction accuracy decreases in the presence of large relative variogram range-related nonstationarity, for the additive trend and residual model-related nonstationarity, the relative prediction errors increase for high trend variance proportions with a decrease in variogram range; regarding the mixture population model-related nonstationarity, the predictions are closer to the smaller variogram range. Common forms of geostatistical nonstationarity may impact CNN predictions, as with geostatistical estimation methods, trend removal and workflows with stationary residuals are recommended.
This is a preview of subscription content, log in via an institution to check access.
Access this article
Subscribe and save
Springer+ Basic
€32.70 /Month
- Get 10 units per month
- Download Article/Chapter or eBook
- 1 Unit = 1 Article or 1 Chapter
- Cancel anytime
Buy Now
Price includes VAT (France)
Instant access to the full article PDF.
Rent this article via DeepDyve
Similar content being viewed by others
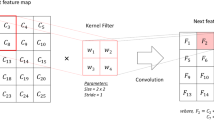
Automatic Semivariogram Modeling by Convolutional Neural Network
Article 12 July 2021

Estimating Spatial Correlation Statistics from CPT Field Data, Using Convolutional Neural Networks and Random Fields
Chapter © 2021
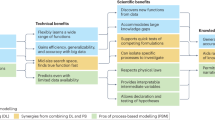
Differentiable modelling to unify machine learning and physical models for geosciences
Article 11 July 2023
Explore related subjects
References
- Pyrcz, M., Deutsch, C.V.: Geostatistical reservoir modeling. New York, New York : Oxford University Press, Oxford (2014) Google Scholar
- Meul, M., Van Meirvenne, M.: Kriging soil texture under different types of nonstationarity. Geoderma. 112, 217–233 (2003). https://doi.org/10.1016/S0016-7061(02)00308-7ArticleGoogle Scholar
- Cressie, N.: Kriging nonstationary data. J. Am. Stat. Assoc. 81, 625–634 (1986). https://doi.org/10.1080/01621459.1986.10478315ArticleGoogle Scholar
- Prokoph, A., Barthelmes, F.: Detection of nonstationarities in geological time series: wavelet transform of chaotic and cyclic sequences. Comput. Geosci. 22, 1097–1108 (1996). https://doi.org/10.1016/S0098-3004(96)00054-4ArticleGoogle Scholar
- Hirsch, R.M.: A perspective on nonstationarity and water Management1. JAWRA J. Am. Water Resour. Assoc. 47, 436–446 (2011). https://doi.org/10.1111/j.1752-1688.2011.00539.xArticleGoogle Scholar
- van Thienen-Visser, K., Breunese, J.N.: Induced seismicity of the Groningen gas field: history and recent developments. Lead. Edge. 34, 664–671 (2015). https://doi.org/10.1190/tle34060664.1ArticleGoogle Scholar
- Cuba, M.A., Leuangthong, O., Ortiz, J.M.: Detecting and quantifying sources of non-stationarity via experimental semivariogram modeling. Stoch. Env. Res. Risk A. 26, 247–260 (2012). https://doi.org/10.1007/s00477-011-0501-9ArticleGoogle Scholar
- Salazar, J.J., Garland, L., Ochoa, J., Pyrcz, M.J.: Fair train-test split in machine learning: mitigating spatial autocorrelation for improved prediction accuracy. J. Pet. Sci. Eng. 209, 109885 (2021). https://doi.org/10.1016/j.petrol.2021.109885ArticleGoogle Scholar
- Leung, Y., Mei, C.-L., Zhang, W.-X.: Statistical tests for spatial nonstationarity based on the geographically weighted regression model. Environ. Plan. Econ. Space. 32, 9–32 (2000). https://doi.org/10.1068/a3162ArticleGoogle Scholar
- Atkinson, P.M., Lloyd, C.D.: Non-stationary variogram models for geostatistical sampling optimisation: an empirical investigation using elevation data. Comput. Geosci. 33, 1285–1300 (2007). https://doi.org/10.1016/j.cageo.2007.05.011ArticleGoogle Scholar
- Vieira, S., Hatfield, J., Nielsen, D., Biggar, J.: Geostatistical theory and application to variability of some agronomical properties. Hilgardia. 51, 1–75 (1983) ArticleGoogle Scholar
- Vieira, S.R., de Carvalho, J.R.P., Ceddia, M.B., González, A.P.: Detrending non stationary data for geostatistical applications. Bragantia. 69, 01–08 (2010). https://doi.org/10.1590/S0006-87052010000500002ArticleGoogle Scholar
- Deutsch, C.V., Journel, A.G.: GSLIB: geostatistical software library and User’s guide. Oxford University Press (1992)
- Santos, J.E., Yin, Y., Jo, H., Pan, W., Kang, Q., Viswanathan, H.S., Prodanović, M., Pyrcz, M.J., Lubbers, N.: Computationally efficient multiscale neural networks applied to fluid flow in complex 3D porous media. Transp. Porous Media. 140, 241–272 (2021). https://doi.org/10.1007/s11242-021-01617-yArticleGoogle Scholar
- Jo, H., Pyrcz, M.J.: Automatic Semivariogram modeling by convolutional neural network. Math. Geosci. 54, 177–205 (2022). https://doi.org/10.1007/s11004-021-09962-wArticleGoogle Scholar
- Imamverdiyev, Y., Sukhostat, L.: Lithological facies classification using deep convolutional neural network. J. Pet. Sci. Eng. 174, 216–228 (2019). https://doi.org/10.1016/j.petrol.2018.11.023ArticleGoogle Scholar
- Li, Z., Meier, M.-A., Hauksson, E., Zhan, Z., Andrews, J.: Machine learning seismic wave discrimination: application to earthquake early warning. Geophys. Res. Lett. 45, 4773–4779 (2018). https://doi.org/10.1029/2018GL077870ArticleGoogle Scholar
- Dramsch, J.S., Lüthje, M., Christensen, A.N.: Complex-valued neural networks for machine learning on non-stationary physical data. Comput. Geosci. 146, 104643 (2021). https://doi.org/10.1016/j.cageo.2020.104643ArticleGoogle Scholar
- Yamashita, R., Nishio, M., Do, R.K.G., Togashi, K.: Convolutional neural networks: an overview and application in radiology. Insights Imaging. 9, 611–629 (2018). https://doi.org/10.1007/s13244-018-0639-9ArticleGoogle Scholar
- Krizhevsky, A., Sutskever, I., Hinton, G.E.: ImageNet classification with deep convolutional neural networks. Commun. ACM. 60, 84–90 (2017). https://doi.org/10.1145/3065386ArticleGoogle Scholar
- Zhang, T.-F., Tilke, P., Dupont, E., Zhu, L.-C., Liang, L., Bailey, W.: Generating geologically realistic 3D reservoir facies models using deep learning of sedimentary architecture with generative adversarial networks. Pet. Sci. 16, 541–549 (2019). https://doi.org/10.1007/s12182-019-0328-4ArticleGoogle Scholar
- Jung, K., Shah, N.H.: Implications of non-stationarity on predictive modeling using EHRs. J. Biomed. Inform. 58, 168–174 (2015). https://doi.org/10.1016/j.jbi.2015.10.006ArticleGoogle Scholar
- Solomon, J., Lyu, P., Marin, D., Samei, E.: Noise and spatial resolution properties of a commercially available deep learning-based CT reconstruction algorithm. Med. Phys. 47, 3961–3971 (2020). https://doi.org/10.1002/mp.14319ArticleGoogle Scholar
- Gómez-Hernández, J.J., Cassiraga, E.F.: Theory and practice of sequential simulation. In: Armstrong, M., Dowd, P.A. (eds.) Geostatistical Simulations, pp. 111–124. Springer Netherlands, Dordrecht (1994) ChapterGoogle Scholar
- Verly, G.: Sequential Gaussian simulation: a Monte Carlo method for generating models of porosity and permeability. In: Spencer, A.M. (ed.) Generation, Accumulation and Production of Europe’s Hydrocarbons III, pp. 345–356. Springer, Berlin Heidelberg, Berlin, Heidelberg (1993) ChapterGoogle Scholar
- Chen, F., Chen, S., Peng, G.: Using sequential Gaussian simulation to assess geochemical anomaly areas of Lead element. In: Li, D., Chen, Y. (eds.) Computer and Computing Technologies in Agriculture VI, pp. 69–76. Springer, Berlin, Heidelberg (2013) ChapterGoogle Scholar
- Mowrer, H.T.: Propagating uncertainty through spatial estimation processes for old-growth subalpine forests using sequential Gaussian simulation in GIS. Ecol. Model. 98, 73–86 (1997). https://doi.org/10.1016/S0304-3800(96)01938-2ArticleGoogle Scholar
- Delbari, M., Afrasiab, P., Loiskandl, W.: Using sequential Gaussian simulation to assess the field-scale spatial uncertainty of soil water content. CATENA. 79, 163–169 (2009). https://doi.org/10.1016/j.catena.2009.08.001ArticleGoogle Scholar
- Nussbaumer, R., Mariethoz, G., Gloaguen, E., Holliger, K.: Which path to choose in sequential Gaussian simulation. Math. Geosci. 50, 97–120 (2018). https://doi.org/10.1007/s11004-017-9699-5ArticleGoogle Scholar
- Frykman, P., Deutsch, C.V.: Geostatistical Scaling Laws Applied to Core and Log Data. Presented at the SPE Annual Technical Conference and Exhibition, Houston, Texas, (October 1999). https://doi.org/10.2118/56822-MS
- LeCun, Y., Bengio, Y., Hinton, G.: Deep learning. Nature. 521, 436–444 (2015). https://doi.org/10.1038/nature14539ArticleGoogle Scholar
- Albawi, S., Mohammed, T. A., Al-Zawi, S.: Understanding of a convolutional neural network. In: 2017 International Conference on Engineering and Technology (ICET). pp. 1–6 (2017). https://doi.org/10.1109/ICEngTechnol.2017.8308186
- Chauhan, R., Ghanshala, K.K., Joshi, R.C.: Convolutional Neural Network (CNN) for Image Detection and Recognition. In: 2018 First International Conference on Secure Cyber Computing and Communication (ICSCCC), Jalandhar, India, pp. 278–282 (2018). https://doi.org/10.1109/ICSCCC.2018.8703316
- Gu, J., Wang, Z., Kuen, J., Ma, L., Shahroudy, A., Shuai, B., Liu, T., Wang, X., Wang, G., Cai, J., Chen, T.: Recent advances in convolutional neural networks. Pattern Recogn. 77, 354–377 (2018). https://doi.org/10.1016/j.patcog.2017.10.013ArticleGoogle Scholar
- Wang, Q., Ma, Y., Zhao, K., Tian, Y.: A comprehensive survey of loss functions in machine learning. Ann. Data Sci. 9, 187–212 (2022). https://doi.org/10.1007/s40745-020-00253-5ArticleGoogle Scholar
Acknowledgments
The authors thank the Digital Reservoir Characterization Technology (DIRECT) Industry Affiliate Program at the University of Texas at Austin for supporting this work.
Author information
Authors and Affiliations
- Hildebrand Department of Petroleum and Geosystems Engineering, The University of Texas at Austin, Austin, TX, USA Lei Liu, Maša Prodanović & Michael J. Pyrcz
- Jackson School of Geosciences, The University of Texas at Austin, Austin, TX, USA Michael J. Pyrcz
- Lei Liu



